[프로그래머스 Level.2] 하노이의 탑 (연습문제) (Java)

문제 링크

https://school.programmers.co.kr/learn/courses/30/lessons/12946

프로그래머스

 

 

 

코딩테스트 연습 > 연습문제 > 하노이의 탑

 

 

 

문제 설명

 

 

하노이 탑(Tower of Hanoi)은 퍼즐의 일종입니다. 세 개의 기둥과 이 기동에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있습니다. 게임의 목적은 다음 두 가지 조건을 만족시키면서, 한 기둥에 꽂힌 원판들을 그 순서 그대로 다른 기둥으로 옮겨서 다시 쌓는 것입니다.

 

1. 한 번에 하나의 원판만 옮길 수 있습니다.
2. 큰 원판이 작은 원판 위에 있어서는 안됩니다.

 

하노이 탑의 세 개의 기둥을 왼쪽 부터 1번, 2번, 3번이라고 하겠습니다. 1번에는 n개의 원판이 있고 이 n개의 원판을 3번 원판으로 최소 횟수로 옮기려고 합니다.

 

1번 기둥에 있는 원판의 개수 n이 매개변수로 주어질 때, n개의 원판을 3번 원판으로 최소로 옮기는 방법을 return하는 solution를 완성해주세요.

 

 

 

제한사항

 

• n은 15이하의 자연수 입니다.

 

---

 

입출력 예

 

n	result
2	[ [1,2], [1,3], [2,3] ]

 

 

입출력 예 설명

 

입출력 예 #1

다음과 같이 옮길 수 있습니다.

 

 

 

 

 

 

 

 

 

 

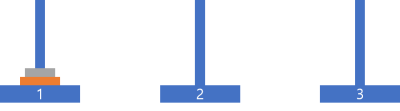
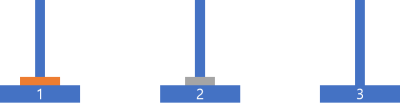
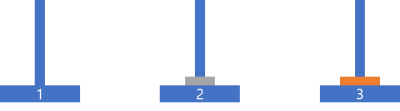
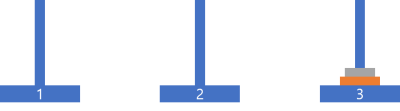
나의 코드

import java.util.*;

class Solution {
    ArrayList<int[]> list;
	
    public int[][] solution(int n) {
        list = new ArrayList<>();
        
        hanoi(n, 1, 2, 3);
        
        int[][] answer = new int[list.size()][2];
        
        for(int i = 0; i < list.size(); i++) {
            answer[i][0] = list.get(i)[0];
            answer[i][1] = list.get(i)[1];
        }
        
        return answer;
    }
    
    public void hanoi(int n, int from, int via, int to) {
        int[] move = {from, to};
		
        if(n == 1) {
            System.out.println(n + "번 원반을 " + "\'" + move[0] + "\'" + "에서 " + "\'" + move[1] + "\'" + "로 옮긴다.");
            list.add(move);
        } else {
            hanoi(n-1, from, to, via);
            System.out.println(n + "번 원반을 " + "\'" + move[0] + "\'" + "에서 " + "\'" + move[1] + "\'" + "로 옮긴다.");
            list.add(move);
            hanoi(n-1, via, from, to);
        }
    }
	
}

 

풀이

1. 하노이의 탑은 세 개의 기둥('A', 'B', 'C')이 있다면 'A'에 n개의 원판이 있을 때 한 번에 하나의 원반을 이동시키고 큰 원판이 작은 원판 위에 있으면 안되는 규칙을 지키면서   A'에서 'C'로 원반을 모두 이동시키는 것이다. 
2. 우선 원반이 이동 할 때마다 담아줄 List를 생성한다. from에서 to로 이동하도록 만들기 위해 int형 배열을 선언타입으로 하는 리스트를 생성한다.
3. 그리고 3개의 기둥을 이용하여 n개의 원반을 from에서 via를 거쳐 to로 이동하는 hanoi()를 구현한다. hanoi(n, 1, 2, 3)은 n개의 원반을 1에서 ~해서 3으로 이동하라를 뜻한다.
4. n개의 원반을 1에서 3으로 이동하기 위해서는 이동할 때 큰 원반이 작은 원반 위에 있으면 안된다는 규칙을 지키기 위해서는 n-1개의 원반은 2에 있어야 하고 1에 있는 제일 큰 마지막 한개의 원반만 3으로 이동시키도록 해야 한다. 그리고 또 나머지 n-2개의 원반을 1로 이동시켜야 두 번째로 큰 원반을 2에서 3으로 이동시킬 수 있다. 이런식으로 원반이 이동해야 하기 때문에 n이 1이 될때까지 재귀 호출을 진행하도록 한다.
5. 즉, n이 1일 때는 1번 원반을 from에서 to로 이동시키고 n이 1이 아닐 때는 hanoi(n-1, from, via, to)를 호출하고 n번 원반을 from에서 to로 이동시키고 다시 hanoi(n-1, via, from, to)를 호출하도록 한다.
   결국 이것은 첫 번째 재귀에서 맨 밑에 있는 n번째 원반을 목적지로 옮기기 위해 위의 n-1 개의 원반을 경유지로 옮기고 그 다음에 n번째 원반을 목적지로 옮긴 후에 다시 경유지에 있는 n-1 개의 원반을 to로 옮기는 것이다.
6. 이렇게 hanoi()를 재귀 호출하면서 조건을 만족시키면서 원반이 이동하는 것을 int형 배열 move에 출발 기둥, 도착 기둥을 담고 리스트에 담아준다. 원반을 모두 이동시키면 move를 모두 담은 List를 for문을 돌면서 answer에 담아주고 반환한다.

 

참고 : https://shoark7.github.io/programming/algorithm/tower-of-hanoi