[프로그래머스 Level.4] 행렬과 연산 (2022 KAKAO TECH INTERNSHIP) (Java)
문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/118670
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
코딩테스트 연습 > 2022 KAKAO TECH INTERNSHIP > 행렬과 연산
문제 설명
[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]
당신은 행렬에 적용할 수 있는 두 가지 연산을 만들었습니다.
- ShiftRow
- 모든 행이 아래쪽으로 한 칸씩 밀려납니다. 즉, 모든 행에 대해서 i번째 행은 i+1번째 행이 됩니다. (마지막 행은 1번째 행이 됩니다.)
- ShiftRow의 예

- 왼쪽 행렬이 초기 상태이고 오른쪽 행렬이 ShiftRow를 한 번 시행한 뒤의 행렬입니다.
- 1번째 행에 있던 [1,2,3]이 2번째 행으로, 2번째 행에 있던 [4,5,6]이 3번째 행으로, 3번째 행에 있던 [7,8,9]가 1번째 행이 된 것을 확인할 수 있습니다.
- Rotate
- 행렬의 바깥쪽에 있는 원소들을 시계 방향으로 한 칸 회전시킵니다.
- 행렬의 바깥쪽에 있는 원소들은 첫 행, 첫 열, 끝 행, 끝 열에 포함되는 원소들입니다.
- 한 칸 회전시킨다는 것은 이 원소들이 시계 방향으로 한 칸씩 밀려난다는 것을 의미합니다. 즉, 다음 4개의 연산이 동시에 시행됩니다.
- 첫 행에서 끝 열에 있는 원소를 제외한 첫 행의 모든 원소는 오른쪽으로 한 칸 이동합니다.
- 끝 열에서 끝 행에 있는 원소를 제외한 끝 열의 모든 원소는 아래쪽으로 한 칸 이동합니다.
- 끝 행에서 첫 열에 있는 원소를 제외한 끝 행의 모든 원소는 왼쪽으로 한 칸 이동합니다.
- 첫 열에서 첫 행에 있는 원소를 제외한 첫 열의 모든 원소는 위쪽으로 한 칸 이동합니다.
- Rotate의 예

- 왼쪽 행렬이 초기 상태이고 오른쪽 행렬이 Rotate를 한 번 시행한 뒤의 행렬입니다.
- 바깥쪽에 있는 값들이 시계 방향으로 한 칸씩 이동한 것을 확인할 수 있습니다.
당신은 행렬에 연산을 여러 번 시행하려고 합니다.
행렬의 초기 상태를 담고 있는 2차원 정수 배열 rc, 시행할 연산을 순서대로 담고 있는 문자열 배열 operations가 매개변수로 주어졌을 때, 연산을 차례대로 시행한 후의 행렬 상태를 return 하도록 solution 함수를 완성해주세요.
- 2 ≤ rc의 행 길이(=행렬의 가로 길이) ≤ 50,000
- rc의 모든 행의 길이는 동일합니다.
- 2 ≤ rc의 열 길이(=행렬의 세로 길이) ≤ 50,000
- rc의 모든 열의 길이는 동일합니다.
- 4 ≤ rc의 행 길이 x rc의 열 길이 ≤ 100,000
- rc[i][j] 는 i+1번째 행 j+1번째 열에 있는 원소를 나타냅니다.
- 1 ≤ rc[i][j] ≤ 1,000,000
- 1 ≤ operations의 길이 ≤ 100,000
- operations의 원소는 "ShiftRow" 혹은 "Rotate"입니다.
정확성 테스트 케이스 제한 사항
- 2 ≤ rc의 행 길이(=행렬의 가로 길이) ≤ 1,000
- rc의 모든 행의 길이는 동일합니다.
- 2 ≤ rc의 열 길이(=행렬의 세로 길이) ≤ 1,000
- rc의 모든 열의 길이는 동일합니다.
- 4 ≤ rc의 행 길이 x rc의 열 길이 ≤ 10,000
- 1 ≤ operations의 길이 ≤ 100
효율성 테스트 케이스 제한 사항
- 주어진 조건 외 추가 제한사항 없습니다.
입출력 예
| rc | operations | result |
| [[1, 2, 3], [4, 5, 6], [7, 8, 9]] | ["Rotate", "ShiftRow"] | [[8, 9, 6], [4, 1, 2], [7, 5, 3]] |
| [[8, 6, 3], [3, 3, 7], [8, 4, 9]] | ["Rotate", "ShiftRow", "ShiftRow"] | [[8, 3, 3], [4, 9, 7], [3, 8, 6]] |
| [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]] | ["ShiftRow", "Rotate", "ShiftRow", "Rotate"] | [[1, 6, 7 ,8], [5, 9, 10, 4], [2, 3, 12, 11]] |
입출력 예#1

위 그림은 ”Rotate”와 ”ShiftRow”를 차례대로 실행한 결과입니다.
따라서 [[8, 9, 6], [4, 1, 2], [7, 5, 3]]을 return 해야 합니다.
입출력 예#2

위 그림은 ”Rotate”, ”ShiftRow”, "ShiftRow"를 차례대로 실행한 결과입니다.
따라서 [[8, 3, 3], [4, 9, 7], [3, 8, 6]]을 return 해야 합니다.
입출력 예#3
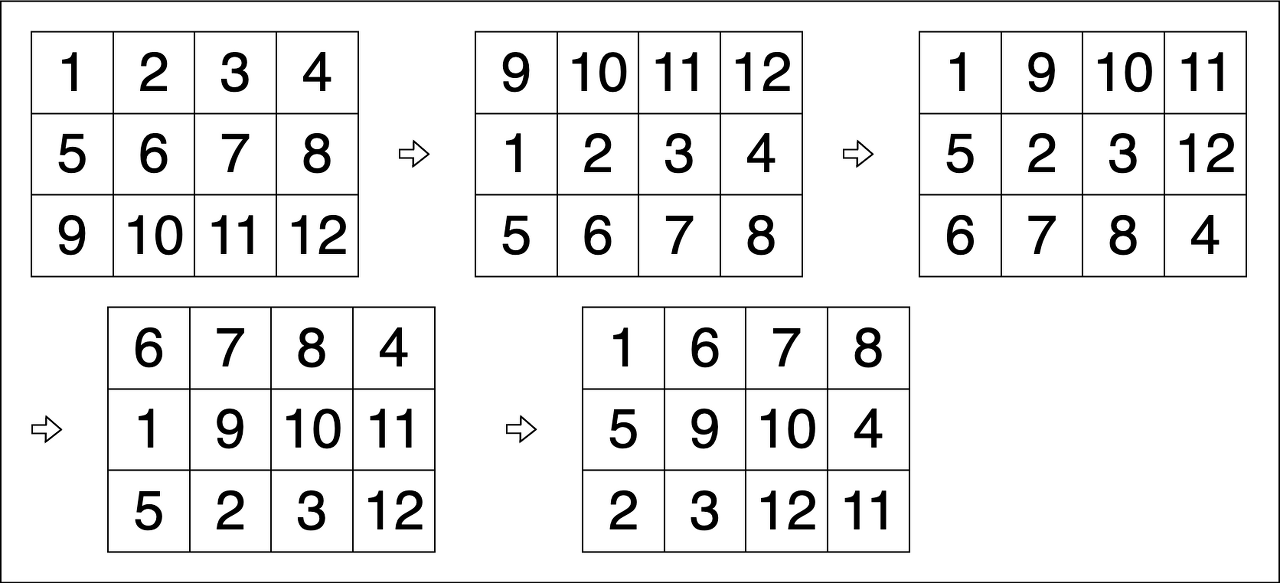
위 그림은 ”ShiftRow”, ”Rotate”, ”ShiftRow”, ”Rotate”를 차례대로 실행한 결과입니다.
따라서 [[1, 6, 7 ,8], [5, 9, 10, 4], [2, 3, 12, 11]]을 return 해야 합니다.
제한시간 안내
- 정확성 테스트 : 10초
- 효율성 테스트 : 언어별로 작성된 정답 코드의 실행 시간의 적정 배수
나의 코드
import java.util.*;
// LinkedList의 경우 삽입삭제는 O(1)이지만 리스트중 맨 마지막 값을 가져오는 get() 연산은 O(n)이 걸림 -> 순차탐색
// Rotate, Shift 연산할 때 필연적으로 get()을 쓰게되니 O(1)이 될 수 없음
class Solution {
Deque<Integer> leftDq;
Deque<Integer> rightDq;
Deque<Deque<Integer>> midDq;
public int[][] solution(int[][] rc, String[] operations) {
int[][] answer = new int[rc.length][rc[0].length];
leftDq = new LinkedList<>();
rightDq = new LinkedList<>();
midDq = new LinkedList<>();
for(int i=0; i<rc.length; i++) {
midDq.addLast(new LinkedList<>());
for(int j=0; j<rc[0].length; j++) {
if(j == 0)
leftDq.addLast(rc[i][j]);
else if(j == rc[0].length-1)
rightDq.addLast(rc[i][j]);
else
midDq.peekLast().addLast(rc[i][j]);
}
}
for(int i=0; i<operations.length; i++) {
if("ShiftRow".equals(operations[i]))
shiftRowRc();
if("Rotate".equals(operations[i]))
rotateRc();
}
for(int i=0; i<rc.length; i++) {
answer[i][0] = leftDq.removeFirst();
answer[i][rc[0].length-1] = rightDq.removeFirst();
int j = 1;
for(int n : midDq.removeFirst())
answer[i][j++] = n;
}
return answer;
}
private void shiftRowRc() {
leftDq.addFirst(leftDq.pollLast());
rightDq.addFirst(rightDq.pollLast());
midDq.addFirst(midDq.pollLast());
}
private void rotateRc() {
midDq.peekFirst().addFirst(leftDq.pollFirst());
rightDq.addFirst(midDq.peekFirst().pollLast());
midDq.peekLast().addLast(rightDq.pollLast());
leftDq.addLast(midDq.peekLast().pollFirst());
}
}
// 최초 시도 - 빡센 효율성 체크로 인해 실패..
class Solution1 {
public int[][] solution(int[][] rc, String[] operations) {
int[][] answer = new int[rc.length][rc[0].length];
for(int i=0; i<operations.length; i++) {
if("ShiftRow".equals(operations[i]))
shiftRowRc(rc);
if("Rotate".equals(operations[i]))
rotateRc(rc);
}
answer = rc;
return answer;
}
// 행을 한칸씩 아래로 이동
private int[][] shiftRowRc(int[][] rc) {
int[] lastRow = rc[rc.length-1];
for(int i=rc.length-1; i>=1; i--)
rc[i] = rc[i-1];
rc[0] = lastRow;
return rc;
}
// 행렬의 테두리 시계방향 회전
// 시계 방향으로 회전하면 첫 꼭지점을 임시로 저장해 놓고
// 왼쪽 테두리부터 반시계 방향 순으로 테두리들을 업데이트 하면서
// 해당 테두리 내부에서도 반시계 방향으로 업데이트 해주면 된다
private int[][] rotateRc(int[][] rc) {
int temp = rc[0][0];
// 왼쪽 테두리
for(int i=0; i<rc.length-1; i++)
rc[i][0] = rc[i+1][0];
// 아래 테두리
for(int i=0; i<rc[0].length-1; i++)
rc[rc.length-1][i] = rc[rc.length-1][i+1];
// 오른쪽 테두리
for(int i=rc.length-1; i>=1; i--)
rc[i][rc[0].length-1] = rc[i-1][rc[0].length-1];
// 위 테두리
for(int i=rc[0].length-1; i>=1; i--)
rc[0][i] = rc[0][i-1];
// 왼쪽 테두리 업데이트 할 때 rc[0][0]이 변경 되었기 때문에 기존 rc[0][0]을 저장해두었던 temp로 rc[0][1]을 다시 업데이트
rc[0][1] = temp;
return rc;
}
}
풀이
- 기존에 행렬 연산 풀이를 했던 것처럼 rotate의 경우 행렬의 바깥쪽 테두리를 한 칸 한 칸씩 이동시켜 행렬을 업데이트 하고 shiftRow의 경우 마지막 행을 임시로 저장해두고 행을 한 칸씩 아래로 이동시킨 후 첫 행에 임시로 저장해두었던 마지막 행을 저장해서 문제를 풀었지만 level4 문제 답게 빡센 효율성 검사로 실패했다..
- 그래서 고민을 해보다가 검색을 해보고 Deque를 이용한 풀이를 찾게되었다.
- 우선 행렬의 제일 좌측 열을 담을 leftDq, 중간의 모든 데이터들을 담을 midDq, 제일 우측 열의 데이터들을 담을 rightDq 이렇게 세 개의 Deque를 생성한다.
- midDq의 경우 제일 좌측 열과 제일 우측 열을 제외한 중간의 모든 데이터들을열 담을 것이므로 Deque를 선언타입으로 갖는 Deque로 생성한다. midDq에는 첫 열과 마지막 열을 제외한 중간 데이터들을 한 행씩 갖게 된다.
예를들어 행렬이 [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]] 라면
leftDq는 첫 행인 [1, 5, 9]이 담기고
rightDq는 마지막 행인 [4, 8, 12]가 담기고
midDq는 [[2, 3], [6, 7], [10, 11]] 이렇게 첫 열과 마지막 열을 제외한 데이터들을 한 행씩 담은 Deque들을 갖는 Deque가 된다. - 이렇게 rc를 이중 for문을 돌면서 모든 데이터를 담는다. 행이 바뀔 때마다 midDq에 새로운 Deque를 생성하고 j=0 일 때는 첫 열이므로 leftDq에 데이터들을 담고 j = rc.length-1일 때는 마지막 열이므로 rightDq에 데이터들을 담고 중간의 데이터들은 Deque에 해당 행의 j=1일 때부터 j=rc.length-2 까지를 담고 이 Deque를 midDq에 담는다.
- 그리고 주어진 operations를 for문을 돌면서 "ShiftRow" 일 때와 "Rotate"일 때를 나눠 분기처리한다.
- ShiftRow일 때는 leftDq, midDq, rightDq 각각 마지막 데이터를 꺼내서 제일 처음 차리로 넣어준다.
leftDq와 rightDq의 경우 마지막 데이터를 처음 자리로 넣어주는 것이고 midDq의 경우 마지막 행의 데이터를 갖고있는 Deque를 꺼내서 처음 자리로 넣어주는 것이다. - Rotate의 경우에는 맨 왼쪽 위쪽 테두리부터 순서대로 시계방향으로 한 칸씩 옮긴다.
예를들어 행렬이 [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]로 예를 들어보자.
첫 번째로 leftDq의 첫 데이터를 꺼내서 midDq의 첫 번째 Deque의 첫 번째 데이터로 넣어준다.
leftDq = [1, 5, 9], midDq = [[2, 3], [6, 7], [10, 11]], rightDq = [4, 8, 12] 에서
leftDq = [5, 9], midDq = [[1, 2, 3], [6, 7], [10, 11]], rightDq = [4, 8, 12] 가 된다.
두 번째로 midDq의 첫 번째 Deque의 마지막 데이터를 rightDq의 첫 번째 데이터로 넣어준다.
leftDq = [5, 9], midDq = [[1, 2, 3], [6, 7], [10, 11]], rightDq = [4, 8, 12] 에서
leftDq = [5, 9], midDq = [[1, 2], [6, 7], [10, 11]], rightDq = [3, 4, 8, 12] 가 된다.
세 번째로 rightDq의 마지막 데이터를 midDq의 마지막 Deuqe의 마지막 데이터로 넣어준다.
leftDq = [5, 9], midDq = [[1, 2], [6, 7], [10, 11]], rightDq = [3, 4, 8, 12] 에서
leftDq = [5, 9], midDq = [[1, 2], [6, 7], [10, 11, 12]], rightDq = [3, 4, 8] 가 된다.
네 번째로 midDq의 마지막 Deque의 첫 번째 데이터를 leftDq의 마지막 데이터로 넣어준다.
leftDq = [5, 9], midDq = [[1, 2], [6, 7], [10, 11, 12]], rightDq = [3, 4, 8] 에서
leftDq = [5, 9, 10], midDq = [[1, 2], [6, 7], [11, 12]], rightDq = [3, 4, 8] 가 된다.
따라서 행렬의 테두리를 시계 방향으로 한 칸씩 이동한 [[5, 1, 2, 3], [9, 6, 7, 4], [10, 11, 12, 8]]가 된다. - 이렇게 operations을 for문을 돌면서 leftDq, midDq, rightDq를 이용하여 ShiftRow일 때와 Rotate일 경우를 모두 처리한 후에 최종적으로 변환된 leftDq, midDq, rightDq를 이용하여 다시 행렬을 만든다.
- 행렬의 행마다 leftDq에서 첫 데이터를 꺼내어 첫 열 자리에 넣고 midDq의 첫 Deque를 꺼내어 두 번째 열부터 마지막에서 하나 전 열까지 넣고 마지막 열 자리에 rightDq의 첫 데이터를 꺼내어 넣는다.
- 이렇게 answer에 새로운 행렬을 만들어 저장한 후 반환한다.
