Programmers
[프로그래머스 Level.3] 섬 연결하기 (탐욕법(Greedy)) (Java)
Devtraces
2023. 3. 31. 12:41
문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/42861
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
코딩테스트 연습 > 탐욕법(Greedy) > 섬 연결하기
문제 설명
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한사항
- 섬의 개수 n은 1 이상 100 이하입니다.
- costs의 길이는 ((n-1) * n) / 2이하입니다.
- 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
- 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
- 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
- 연결할 수 없는 섬은 주어지지 않습니다.
입출력 예
| n | costs | return |
| 4 | [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] | 4 |
입출력 예 설명
costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.
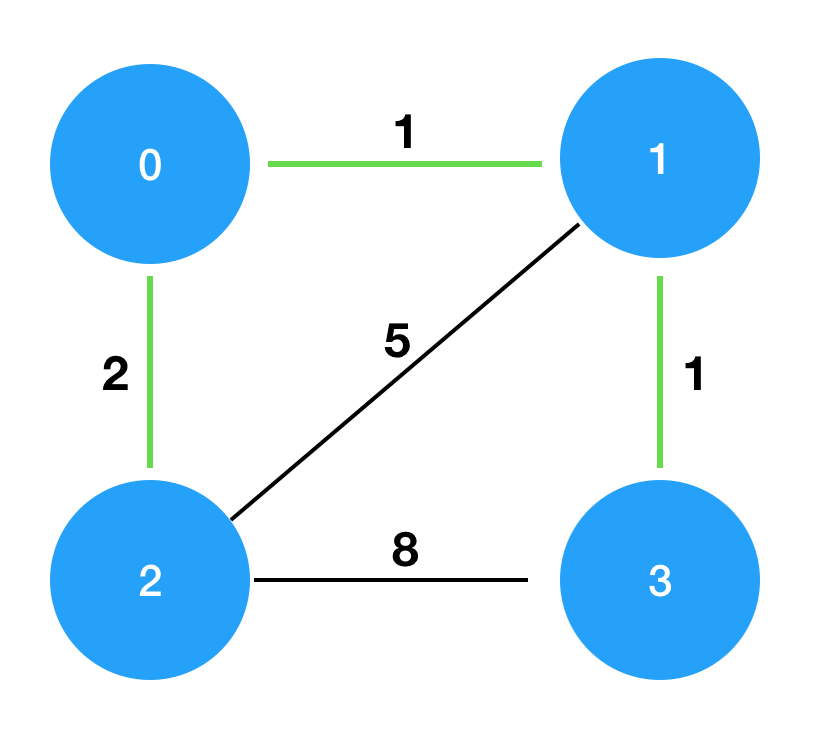
나의 코드
import java.util.*;
// 1. 최소비용으로 모든 섬이 통행 가능하도록 연결시키기
// -> Minimum Spanning Tree(최소 신장 트리)를 만들어라
// 2. Minimum Spanning Tree(최소 신장 트리) : 그래프에서 가중치 무방향 그래프에서 모든 정점을 최소 비용으로 연결한 트리
// -> 최소 비용이 되려면 사이클을 형성하지 않아야 한다. 사이클은 같은 그래프에 속한 두 노드를 연결했을 때 발생한다.
// 3. Kruskal(크루스칼) Algorithm : 음수 가중치가 없는 무방향 그래프에서 Minimum Spanning Tree를 찾는 알고리즘
// -> 가중치가 작은 간선부터 선택하여 사이클을 형성하지 않는지 확인하고 그래프에 포함시켜 최소 신장 트리를 만드는 알고리즘
// 4. Disjoint Set(서로소 집합) 자료구조 - Union Find(합집합 찾기) : 서로 다른 원소들이 같은 집합에 속해있는지, 혹은 속해있지 않은지를 판별하는데 사용
// -> 두 임의의 노드가 같은 그래프에 속하는지 판별하여 사이클을 형성하지 않도록 할 수 있다.
class Solution {
int[] parent;
public int solution(int n, int[][] costs) {
int answer = 0;
// 크루스칼 알고리즘은 가중치가 작은 간선부터 선택하기 때문에 가중치를 기준으로 오름차순 정렬
// Arrays.sort(costs, (int[] o1, int[] o2) -> o1[2] - o2[2]);
Arrays.sort(costs, (o1, o2) -> o1[2] - o2[2]);
// Union Find(disjoint set 합집합 찾기)에 사용하기 위한 배열 생성
parent = new int[n];
// Union Find를 하기 위해 부모(대표 노드)를 모두 자기 자신을 가리키도록 초기화
for(int i=0; i<n; i++) parent[i] = i;
for(int[] edge : costs) {
int from = edge[0];
int to = edge[1];
int cost = edge[2];
// Find
int fromParent = findParent(from);
int toParent = findParent(to);
// 두 노드의 부모(대표 노드)가 같으면(같은 그래프에 속하면) 해당 간선 선택 X
if(fromParent == toParent) continue;
// Union 연산 - 간선을 연결해 두 노드가 같은 그래프에 속하게 함(통상적으로 값이 작은 노드를 부모로 선택)
if(fromParent < toParent)
parent[toParent] = fromParent;
else
parent[fromParent] = toParent;
answer += cost; // 간선을 연결했으므로 가중치 추가
}
return answer;
}
// Find 연산 - 부모가 자기 자신으로 되어있는 노드(대표 노드)를 찾을 때까지 재귀호출
public int findParent(int node) {
if(parent[node] == node) return node;
return findParent(parent[node]);
}
}
풀이
- 문제 풀이에 앞서 이 문제를 풀기 위해서는 Minimum Spanning Tree(최소 신장 트리), Kruskal Algorithm(크루스칼 알고리즘), Disjoint Set(서로소 집합), Union-Find(합집합 찾기)의 개념을 알아야 한다.
- Minimum Spanning Tree(최소 신장 트리) : 그래프에서 가중치 무방향 그래프에서 모든 정점을 최소 비용으로 연결한 트리 -> 최소 비용이 되려면 사이클을 형성하지 않아야 한다. 사이클은 같은 그래프에 속한 두 노드를 연결했을 때 발생한다.
- Kruskal(크루스칼) Algorithm : 음수 가중치가 없는 무방향 그래프에서 Minimum Spanning Tree를 찾는 알고리즘 -> 가중치가 작은 간선부터 선택하여 사이클을 형성하지 않는지 확인하고 그래프에 포함시켜 최소 신장 트리를 만드는 알고리즘이다.
- Disjoint Set(서로소 집합) 자료구조 - Union Find(합집합 찾기) : 서로 다른 원소들이 같은 집합에 속해있는지, 혹은 속해있지 않은지를 판별하는데 사용 -> 두 임의의 노드가 같은 그래프에 속하는지 판별하여 사이클을 형성하지 않도록 할 수 있다.
- 최소비용으로 모든 섬이 통행 가능하도록 연결시키라는 것은 그래프에서 모든 정점을 최소 비용으로 연결하라는 것으로 Minimum Spanning Tree(최소 신장 트리)를 만들라는 것이다.
- 우선 Kruskal Algorithm을 사용하기 위해 주어진 costs를 가중치(연결 비용)를 기준으로 오름차순 정렬한다.
- Union Find에 사용하기 위한 배열 parent를 n길이만큼 생성하고 각각 자기 자신을 가리키도록 초기화한다. (각자 자기 자신을 대표 노드(부모)로 하는 집합이 된다)
- 이제 costs를 for each문을 돌리면서 from 노드와 to 노드의 대표 노드(부모)를 찾아(Find 연산) 두 노드의 대표 노드(부모)가 같으면 현재 두 원소는 같은 그래프(집합)에 속하는 것으로 해당 간선을 선택하지 않아야 되므로 넘어가고 두 노드의 대표 노드(부모)가 다르다면 현재 다른 그래프(집합)에 속하는 것이므로 해당 간선을 연결(Union 연산)하고 answer에 해당 간선의 가중치(연결 비용) 만큼 더해준다.
- 해당 노드의 대표 노드를 찾는 것(Find 연산)은 자기 자신이 대표 노드로 되어 있는 노드를 찾는 것으로 parent[노드]가 자기 자신으로 되어있다면 자기 자신을 반환하고 아니라면 parent[노드]의 값으로 다시 재귀 호출을 하며 대표 노드를 찾을 때까지 parent 배열을 순회한다.
- 두 노드 사이의 간선을 연결하여 같은 그래프(집합)에 속하게 하는 것(Union 연산)은 두 노드의 대표 노드(parent[노드])를 같게 하는 것으로 통상적으로 낮은 쪽이 대표 노드가 되도록 합친다.
- 최종적으로 모든 노드를 최소 비용으로 연결(모든 섬을 최소 비용으로 연결)하며 구한 answer를 반환하면 된다.
참고
서로소 집합, 유니온 파인드 :
https://yoongrammer.tistory.com/102
최소 신장 트리, 크루스칼 알고리즘 :
크루스칼 알고리즘, 유니온 파인드 :
문제 풀이 :