[프로그래머스 Level.3] 등산코스 정하기 (2022 KAKAO TECH INTERNSHIP) (Java)
문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/118669
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
코딩테스트 연습 > 2022 KAKAO TECH INTERNSHIP > 등산코스 정하기
문제 설명
XX산은 n개의 지점으로 이루어져 있습니다. 각 지점은 1부터 n까지 번호가 붙어있으며, 출입구, 쉼터, 혹은 산봉우리입니다. 각 지점은 양방향 통행이 가능한 등산로로 연결되어 있으며, 서로 다른 지점을 이동할 때 이 등산로를 이용해야 합니다. 이때, 등산로별로 이동하는데 일정 시간이 소요됩니다.
등산코스는 방문할 지점 번호들을 순서대로 나열하여 표현할 수 있습니다.
예를 들어 1-2-3-2-1 으로 표현하는 등산코스는 1번지점에서 출발하여 2번, 3번, 2번, 1번 지점을 순서대로 방문한다는 뜻입니다.
등산코스를 따라 이동하는 중 쉼터 혹은 산봉우리를 방문할 때마다 휴식을 취할 수 있으며, 휴식 없이 이동해야 하는 시간 중 가장 긴 시간을 해당 등산코스의 intensity라고 부르기로 합니다.
당신은 XX산의 출입구 중 한 곳에서 출발하여 산봉우리 중 한 곳만 방문한 뒤 다시 원래의 출입구로 돌아오는 등산코스를 정하려고 합니다. 다시 말해, 등산코스에서 출입구는 처음과 끝에 한 번씩, 산봉우리는 한 번만 포함되어야 합니다.
당신은 이러한 규칙을 지키면서 intensity가 최소가 되도록 등산코스를 정하려고 합니다.
다음은 XX산의 지점과 등산로를 그림으로 표현한 예시입니다.
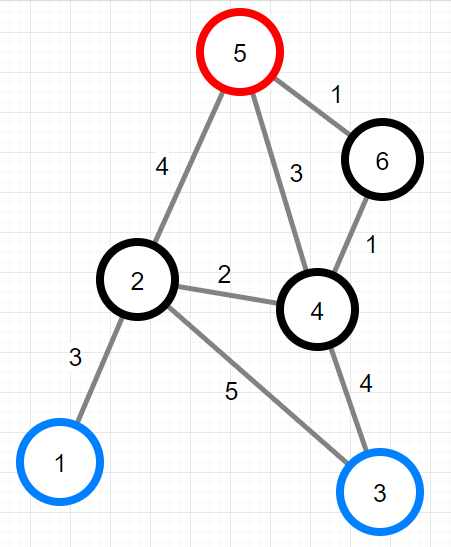
- 위 그림에서 원에 적힌 숫자는 지점의 번호를 나타내며, 1, 3번 지점에 출입구, 5번 지점에 산봉우리가 있습니다. 각 선분은 등산로를 나타내며, 각 선분에 적힌 수는 이동 시간을 나타냅니다. 예를 들어 1번 지점에서 2번 지점으로 이동할 때는 3시간이 소요됩니다.
위의 예시에서 1-2-5-4-3 과 같은 등산코스는 처음 출발한 원래의 출입구로 돌아오지 않기 때문에 잘못된 등산코스입니다. 또한 1-2-5-6-4-3-2-1 과 같은 등산코스는 코스의 처음과 끝 외에 3번 출입구를 방문하기 때문에 잘못된 등산코스입니다.
등산코스를 3-2-5-4-3 과 같이 정했을 때의 이동경로를 그림으로 나타내면 아래와 같습니다.

이때, 휴식 없이 이동해야 하는 시간 중 가장 긴 시간은 5시간입니다. 따라서 이 등산코스의 intensity는 5입니다.
등산코스를 1-2-4-5-6-4-2-1 과 같이 정했을 때의 이동경로를 그림으로 나타내면 아래와 같습니다.

이때, 휴식 없이 이동해야 하는 시간 중 가장 긴 시간은 3시간입니다. 따라서 이 등산코스의 intensity는 3이며, 이 보다 intensity가 낮은 등산코스는 없습니다.
XX산의 지점 수 n, 각 등산로의 정보를 담은 2차원 정수 배열 paths, 출입구들의 번호가 담긴 정수 배열 gates, 산봉우리들의 번호가 담긴 정수 배열 summits가 매개변수로 주어집니다. 이때, intensity가 최소가 되는 등산코스에 포함된 산봉우리 번호와 intensity의 최솟값을 차례대로 정수 배열에 담아 return 하도록 solution 함수를 완성해주세요. intensity가 최소가 되는 등산코스가 여러 개라면 그중 산봉우리의 번호가 가장 낮은 등산코스를 선택합니다.
- 2 ≤ n ≤ 50,000
- n - 1 ≤ paths의 길이 ≤ 200,000
- paths의 원소는 [i, j, w] 형태입니다.
- i번 지점과 j번 지점을 연결하는 등산로가 있다는 뜻입니다.
- w는 두 지점 사이를 이동하는 데 걸리는 시간입니다.
- 1 ≤ i < j ≤ n
- 1 ≤ w ≤ 10,000,000
- 서로 다른 두 지점을 직접 연결하는 등산로는 최대 1개입니다.
- 1 ≤ gates의 길이 ≤ n
- 1 ≤ gates의 원소 ≤ n
- gates의 원소는 해당 지점이 출입구임을 나타냅니다.
- 1 ≤ summits의 길이 ≤ n
- 1 ≤ summits의 원소 ≤ n
- summits의 원소는 해당 지점이 산봉우리임을 나타냅니다.
- 출입구이면서 동시에 산봉우리인 지점은 없습니다.
- gates와 summits에 등장하지 않은 지점은 모두 쉼터입니다.
- 임의의 두 지점 사이에 이동 가능한 경로가 항상 존재합니다.
- return 하는 배열은 [산봉우리의 번호, intensity의 최솟값] 순서여야 합니다.
입출력 예
| n | paths | gates | summits | result |
| 6 | [[1, 2, 3], [2, 3, 5], [2, 4, 2], [2, 5, 4], [3, 4, 4], [4, 5, 3], [4, 6, 1], [5, 6, 1]] | [1, 3] | [5] | [5, 3] |
| 7 | [[1, 4, 4], [1, 6, 1], [1, 7, 3], [2, 5, 2], [3, 7, 4], [5, 6, 6]] | [1] | [2, 3, 4] | [3, 4] |
| 7 | [[1, 2, 5], [1, 4, 1], [2, 3, 1], [2, 6, 7], [4, 5, 1], [5, 6, 1], [6, 7, 1]] | [3, 7] | [1, 5] | [5, 1] |
| 5 | [[1, 3, 10], [1, 4, 20], [2, 3, 4], [2, 4, 6], [3, 5, 20], [4, 5, 6]] | [1, 2] | [5] | [5, 6] |
입출력 예 #1
문제 예시와 같습니다. 등산코스의 intensity가 최소가 되는 산봉우리 번호는 5, intensity의 최솟값은 3이므로 [5, 3]을 return 해야 합니다.
입출력 예 #2
XX산의 지점과 등산로를 그림으로 표현하면 아래와 같습니다.
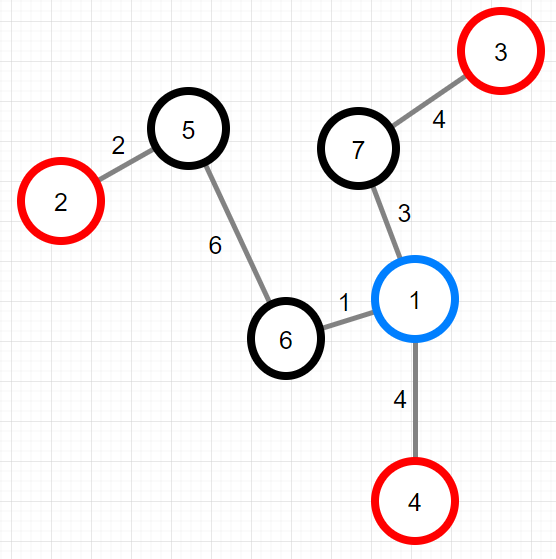
가능한 intensity의 최솟값은 4이며, intensity가 4가 되는 등산코스는 1-4-1 과 1-7-3-7-1 이 있습니다. intensity가 최소가 되는 등산코스가 여러 개이므로 둘 중 산봉우리의 번호가 낮은 1-7-3-7-1 을 선택합니다. 따라서 [3, 4]를 return 해야 합니다.
입출력 예 #3
XX산의 지점과 등산로를 그림으로 표현하면 아래와 같습니다.
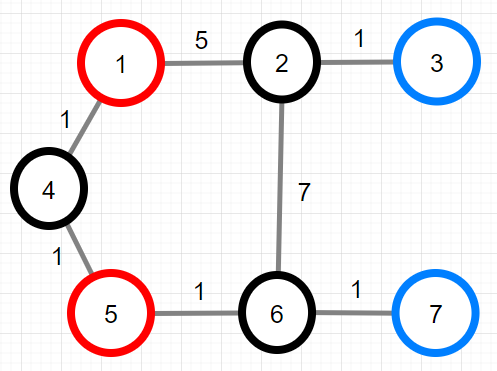
가능한 intensity의 최솟값은 1이며, 그때의 등산코스는 7-6-5-6-7 입니다. 따라서 [5, 1]를 return 해야 합니다.
- 7-6-5-4-1-4-5-6-7 과 같은 등산코스는 산봉우리를 여러 번 방문하기 때문에 잘못된 등산코스입니다.
입출력 예 #4
XX산의 지점과 등산로를 그림으로 표현하면 아래와 같습니다.
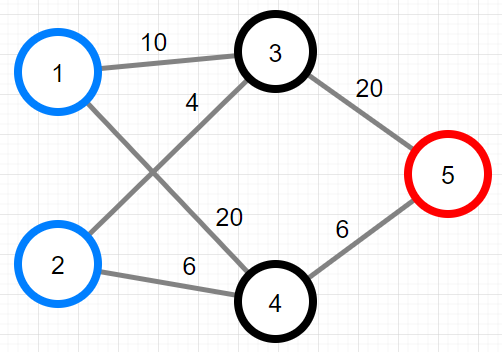
가능한 intensity의 최솟값은 6, 그때의 등산코스는 2-4-5-4-2 입니다. 따라서 [5, 6]을 return 해야 합니다.
나의 코드
import java.util.*;
// 어차피 출입구에서 산봉우리까지 가기만 하면, 돌아오는 길을 그대로 돌아오면 되는거 아님?
// 맞다. 이 문제를 그렇게 풀어야 옳은 문제이다.
// 즉, 돌아오는 길은 굳이 생각하지 않아도 된다. 왜냐고? 이미 가는 길부터 가장 작은 가중치를 가지는 길로 선택해서 지나갈 것이 아닌가?
// 그렇다. 시작과 끝은 항상 같기 때문에, 같은 길로 되돌아오는 것이 가장 최적의 루트가 될 것이라는 것을 쉽게 알 수 있다.
// 이 문제를 풀기 위한 가장 핵심적인 부분 이라고도 할 수 있다.
// 출입구에 연결된 양방향 등산로 -> 출입구에서 다른 지점으로만 이동 가능한 단방향 등산로
// 산봉우리 연결된 양방향 등산로 -> 다른 지점에서 산봉우리로만 이동 가능한 단방향 등산로
// 위와 같이 문제를 바꾼다면 별다른 중복처리 없이 등산코스에서 출입구는 처음과 끝에 한 번씩,
// 산봉우리는 한 번만 포함되어야 하는 규칙을 지킬 수 있습니다.
// 임의의 출입구 A에서 어느 산봉우리로 가야 intensity가 최소가 되는지는 다익스트라 알고리즘을 변형하면
// 쉽게 구할 수 있습니다. 배열 intensity를 다음과 같이 정의합니다.
// intensity[i] = 출입구 A에서 출발하여 i번 지점까지 올 때 가능한 최소 intensity(=등산로들의 가중치 중 최댓값)
class Solution {
ArrayList<ArrayList<Edge>> graph;
public int[] solution(int n, int[][] paths, int[] gates, int[] summits) {
int[] answer = new int[2];
graph = new ArrayList<>();
for(int i=0; i<=n; i++)
graph.add(new ArrayList<>());
// 이렇게 다 넣는게 아니라
// for(int i=0; i<path.length; i++) {
// graph.get(path[i][0]).add(new Edge(path[i][1], path[i][2]));
// graph.get(path[i][1]).add(new Edge(path[i][0], path[i][2]));
// }
// 출입구일 경우 다른 곳으로만 갈 수 있는 단방향
// 산봉우리일 경우 특정 한 곳에서 산봉우리로 가는 단방향
for(int i=0; i<paths.length; i++) {
// 출발지가 게이트이거나 , 도착지가 산봉우리면 단방향만 넣기
if(isGate(paths[i][0], gates) || isSummit(paths[i][1], summits)) {
graph.get(paths[i][0]).add(new Edge(paths[i][1], paths[i][2]));
// 출발지가 산봉우리거나, 도착지가 게이트면 단방향만 넣기
} else if (isGate(paths[i][1], gates) || isSummit(paths[i][0], summits)) {
graph.get(paths[i][1]).add(new Edge(paths[i][0], paths[i][2]));
// 나머지는 양방향 넣기
} else {
graph.get(paths[i][0]).add(new Edge(paths[i][1], paths[i][2]));
graph.get(paths[i][1]).add(new Edge(paths[i][0], paths[i][2]));
}
}
int[] intensities = new int[n+1];
Arrays.fill(intensities, Integer.MAX_VALUE);
answer = dijkstra(gates, summits, intensities);
return answer;
}
public int[] dijkstra(int[] gates, int[] summits, int[] intensities) {
PriorityQueue<Edge> pq = new PriorityQueue<>((o1, o2) -> o1.intensity - o2.intensity);
for(int gate : gates) {
pq.offer(new Edge(gate, 0));
intensities[gate] = 0;
}
while(!pq.isEmpty()) {
Edge nowEdge = pq.poll();
int nIdx = nowEdge.idx;
int nIntensity = nowEdge.intensity;
if(nIntensity > intensities[nIdx])
continue;
ArrayList<Edge> edgeList = graph.get(nIdx);
for(Edge edge : edgeList) {
int intensity = Math.max(intensities[nIdx], edge.intensity);
if(intensities[edge.idx] > intensity) {
intensities[edge.idx] = intensity;
pq.offer(new Edge(edge.idx, intensity));
}
}
}
// intensity가 최소가 되는 등산코스가 여러 개라면 그중 산봉우리의 번호가 가장 낮은 등산코스를 선택
Arrays.sort(summits);
int resSummit = Integer.MAX_VALUE;
int resIntensity = Integer.MAX_VALUE;
for(int summit : summits) {
if(intensities[summit] < resIntensity) {
resSummit = summit;
resIntensity = intensities[summit];
}
}
return new int[]{resSummit, resIntensity};
}
public static boolean isGate(int idx, int[] gates) {
for(int gate : gates) {
if(idx == gate)
return true;
}
return false;
}
public static boolean isSummit(int idx, int[] summits) {
for(int summit : summits) {
if(idx == summit)
return true;
}
return false;
}
class Edge {
int idx;
int intensity;
public Edge(int idx, int intensity) {
this.idx = idx;
this.intensity = intensity;
}
}
}
풀이
- 이 문제는 일반적인 최소이동거리나 최소이동시간을 묻는 문제가 아니라 이동 루트에 속한 노드와 노드 사이의 가중치 중 가장 큰 것(intensity)이 최소가 되는 루트를 구하는 것이다.
- 출입구에서 쉼터들을 거쳐 산봉우리까지 갔다가 다시 쉼터들을 거쳐 출발했던 출발지로 돌아올 필요 없이 거쳐갔던 길을 그대로 돌아오면 되기 때문에 출입구에서 쉼터들을 거쳐 산봉우리까지만 가면 된다. 이때 출입구에서 산봉우리까지 갔을 때 최소의 intensity를 갖는 코스를 찾으면 된다.
- 하나의 출입구에서 출발하면 다른 출입구를 거쳐갈 수 없고 하나의 산봉우리로 도착해야 하기 때문에 출입구에서는 연결된 쉼터로 가는 단방향으로만 갈 수 있고 산봉우리에서는 연결된 쉼터에서 단방향으로만 올 수 있고 나머지는 양방향으로 오고 갈 수 있도록 그래프를 만들어야 한다.
- 따라서 각 지점의 번호 idx와 가중치 intensity를 갖는 Edge 클래스를 생성하고 Edge를 선언타입으로 하는 ArrayList를 원소로 갖는 ArrayList를 생성하여 paths를 순회하면서 그래프를 만든다.
- paths[i][0]가 출입구이거나 paths[i][1]가 산봉우리이면 paths[i][0] -> paths[i][1] 로 단방향으로만 넣고 paths[i][0]가 산봉우리이거나 paths[i][1]이 출입구이면 paths[i][1] -> paths[i][0] 로 단방향으로만 넣고 나머지의 경우는 양방향으로 넣으면 된다.
- 이제 다익스트라 알고리즘을 이용하여 모든 출발지를 우선순위큐에 담고 가중치가 작은 순으로 이동하면서 산봉우리에 도착하며 루트의 최대 가중치(intensity)를 해당 산봉우리에 저장하며 모두 진행하여 산봉우리에 저장된 가중치(intensity) 중에서 최소 가중치를 찾으면 된다.
- 최대한 작은 intensity의 지점으로 이동하며 intensities[산봉우리]의 최솟값을 구하기 위해서 intensities 배열을 생성하고 모두 int형 최댓값으로 초기화한다.
- Edge를 선언타입으로 하고 intensity를 오름차순으로 정렬하는 우선순위큐를 생성하고 gates를 순회하면서 출발지와 가중치를 0으로하는 Edge를 생성하여 우선순위큐에 담고 출발지의 intensities를 0으로 한다.
- 이제 우선순위큐가 빌 때까지 while문을 반복하면서 우선순위큐의 제일 앞에 있는 Edge 데이터를 꺼내서 해당 intensity가 intensities[Edge의 idx] 이하라면 다음 지점으로 이동할 필요가 있으므로 (크면 이미 해당 지점에 더 작은 값으로 이동한 루트가 있으므로 이동할 필요 X) 해당 지점과 연결된 지점들을 그래프에서 찾아 순회한다. 해당 지점과 연결된 지점의 intensity와 현재 지점의 intensities 값을 비교하여 큰 값을 임시로 저장해놓고 연결된 지점의 intensities 값이 임시로 저장해놓은 intensity 값보다 크다면 연결된 지점의 intensities 값을 이 임시로 저장해놓은 intensity 값으로 변경하고 우선순위큐에 연결된 지점의 idx와 이 intensity로 Edge를 생성하여 우선순위큐에 담는다.
(연결된 지점의 가중치와 현재 지점까지의 가중치를 비교하여 큰 값을 임시 intensity로 놓고 연결된 지점까지 이동했을 때 최소 가중치로 저장되어있는 연결된 지점의 intensities 값보다 이 임시 intensity가 작다면 이게 더 작은 intensity를 갖는 루트이므로 해당 intensity로 업데이트하고 이동하는 것이다) - while문이 종료되면 산봉우리까지 최소의 intensity로 이동하며 intensites에 저장했기 때문에 산봉우리에는 최소의 intensity를 갖는 루트의 산봉우리까지의 도착할 때 해당 루트의 가장 큰 intensity가 저장되어있다.
- 그러므로 각 산봉우리를 순회하면서 intensities 값을 확인하여 최솟값으로 저장되어있는 산봉우리를 찾으면 된다. 문제에서 intensity가 최소가 되는 등산코스가 여러 개라면 그중 산봉우리의 번호가 가장 낮은 등산코스를 선택하라고 하였으므로 산봉우리 번호가 작은 지점부터 순회하기 위해 summits를 오름차순 정렬하고 최솟값의 intensity를 갖는 산봉우리 번호와 해당 intensity를 찾아 answer에 저장하고 반환하면 된다.