문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/1832
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
코딩테스트 연습 > 2017 카카오코드 예선 > 보행자 천국
문제 설명
보행자 천국
카카오내비 개발자인 제이지는 시내 중심가의 경로 탐색 알고리즘 개발 업무를 담당하고 있다. 최근 들어 보행자가 자유롭고 편리하게 걸을 수 있도록 보행자 중심의 교통 체계가 도입되면서 도심의 일부 구역은 자동차 통행이 금지되고, 일부 교차로에서는 보행자 안전을 위해 좌회전이나 우회전이 금지되기도 했다. 복잡해진 도로 환경으로 인해 기존의 경로 탐색 알고리즘을 보완해야 할 필요가 생겼다.
도시 중심가의 지도는 m × n 크기의 격자 모양 배열 city_map으로 주어진다. 자동차는 오른쪽 또는 아래 방향으로 한 칸씩 이동 가능하다.
city_map[i][j]에는 도로의 상황을 나타내는 값이 저장되어 있다.
- 0인 경우에는 자동차가 자유롭게 지나갈 수 있다.
- 1인 경우에는 자동차 통행이 금지되어 지나갈 수 없다.
- 2인 경우는 보행자 안전을 위해 좌회전이나 우회전이 금지된다. (왼쪽에서 오던 차는 오른쪽으로만, 위에서 오던 차는 아래쪽으로만 진행 가능하다)
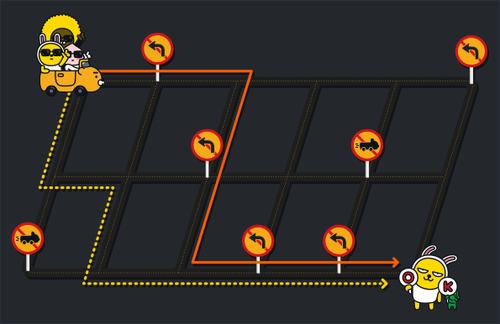
도시의 도로 상태가 입력으로 주어졌을 때, 왼쪽 위의 출발점에서 오른쪽 아래 도착점까지 자동차로 이동 가능한 전체 가능한 경로 수를 출력하는 프로그램을 작성하라. 이때 가능한 경로의 수는 컴퓨터가 표현할 수 있는 정수의 범위를 넘어설 수 있으므로, 가능한 경로 수를 20170805로 나눈 나머지 값을 출력하라.
입력 형식
입력은 도시의 크기를 나타내는 m과 n, 그리고 지도를 나타내는 2차원 배열 city_map으로 주어진다. 제한조건은 아래와 같다.
- 1 <= m, n <= 500
- city_map의 크기는 m × n이다.
- 배열의 모든 원소의 값은 0, 1, 2 중 하나이다.
- 출발점의 좌표는 (0, 0), 도착점의 좌표는 (m - 1, n - 1)이다.
- 출발점과 도착점의 city_map[i][j] 값은 0이다.
출력 형식
출발점에서 도착점까지 이동 가능한 전체 경로의 수를 20170805로 나눈 나머지를 리턴한다.
예제 입출력
| m | n | city_map | answer |
| 3 | 3 | [[0, 0, 0], [0, 0, 0], [0, 0, 0]] | 6 |
| 3 | 6 | [[0, 2, 0, 0, 0, 2], [0, 0, 2, 0, 1, 0], [1, 0, 0, 2, 2, 0]] | 2 |
예제에 대한 설명
첫 번째 예제는 모든 도로가 제한 없이 통행 가능한 경우로, 가능한 경우의 수는 6가지이다.
두 번째 예제는 문제 설명에 있는 그림의 경우이다. 가능한 경우의 수는 빨간 실선과 노란 점선 2가지뿐이다.
나의 코드
import java.util.*;
class Solution {
public int solution(int m, int n, int[][] cityMap) {
int answer = 0;
int MOD = 20170805;
// 밑에 방향 0, 오른쪽 방향 1
int[][][] dp = new int[m][n][2];
dp[0][0][0] = 1; // 해당 위치에 위에서 온 방법의 수
dp[0][0][1] = 1; // 해당 위치에 왼쪽에서 온 방법의 수
// 첫 번째 열 세팅
for(int i=1; i<m; i++) {
if(cityMap[i][0] != 1) dp[i][0][0] = dp[i-1][0][0];
}
// 첫 번째 행 세팅
for(int i=1; i<n; i++) {
if(cityMap[0][i] != 1) dp[0][i][1] = dp[0][i-1][1];
}
for(int i=1; i<m; i++) {
for(int j=1; j<n; j++) {
// 위에서 오는 방법의 수
if(cityMap[i-1][j] == 0) {
dp[i][j][0] = (dp[i-1][j][0] + dp[i-1][j][1]) % MOD;
} else if(cityMap[i-1][j] == 2) {
dp[i][j][0] = dp[i-1][j][0];
}
// 왼쪽에서 오는 방법의 수
if(cityMap[i][j-1] == 0) {
dp[i][j][1] = (dp[i][j-1][0] + dp[i][j-1][1]) % MOD;
} else if(cityMap[i][j-1] == 2) {
dp[i][j][1] = dp[i][j-1][1];
}
}
}
answer = (dp[m-1][n-1][0] + dp[m-1][n-1][1]) % MOD;
return answer;
}
}
풀이
- 출발점부터 목표점까지 갈 수 있는 방법의 수를 구하는 문제로 보통 level.3 등굣길 문제와 같이 dp를 이용하여 왼쪽 좌표까지의 방법의 수와 오른쪽 좌표까지의 방법의 수를 더해가며 풀지만 이 문제는 좌표의 값이 0, 1, 2에 따라 통행이 제한되므로 조금 변형해서 푸는 문제이다. dp를 3차원 배열로 만들어 해당 좌표에 위에서 온 방법의 수를 dp[i][j][0]에 담고 해당 좌표에 왼쪽에서 온 방법의 수를 dp[i][j][1]에 담아 dp를 업데이트 해가며 마지막에 도착점의 dp[m-1][n-1][0]와 dp[m-1][n-1][1]의 값을 더해서 구한다.
- 우선 m * n * 2의 크기로 dp를 3차원 배열로 만들고 첫 번째 좌표(dp[0][0][0], dp[0][0][1])의 값을 1로 세팅한다.
- 그리고 첫 행과 첫 열도 1로 세팅해야 하는데 첫 행은 왼쪽에서만 오는 방법이므로 dp[0][i][1]의 값을 1로 세팅해야 하는데 만약 cityMap[0][i]의 값이 1이라면 통행 제한이기 때문에 해당 좌표가 나오면 해당 좌표부터는 0으로 세팅되도록 한다. 마찬가지로 첫 열은 위에서만 오는 방법이므로 dp[i][0][0]의 값을 1로 세팅해야 하는데 cityMap[i][0]의 값이 1이라면 해당 좌표부터는 0으로 세팅되도록 한다.
- 첫 행과 첫 열의 세팅이 완료되면 나머지 좌표들을 업데이트 하면서 도착점에 도달하면 된다.
- dp[i][j][0]에는 위의 좌표에서 오는 방법의 수를 구하여 업데이트 하고 dp[i][j][1]에는 왼쪽에서 오는 방법의 수를 구하여 업데이트 하도록 한다.
- 우선 위에서 내려오는 방법(dp[i][j][0])을 보면 위의 좌표(cityMap[i-1][j])가 0이라면 위의 좌표에 왼쪽에서 온 방법(dp[i-1][j][1])과 위의 좌표에 위쪽에서 온 방법(dp[i-1][j][0])에서 밑으로 내려오면 되기 때문에 두 방법을 더하고(dp[i-1][j][0] + dp[i-1][j][1]) 수가 커질 수 있기 때문에 문제에서 주어진대로 20170805로 나눈 나머지를 저장한다. (모듈러 연산 법칙에 (A + B) % p = ((A % p) + (B % p)) % p 이기 때문에 계속 나눠서 저장해주도록 한다)
- 또한 위의 좌표(cityMap[i-1][j])가 2라면 위의 좌표에서 좌회전과 우회전이 되지 않기 때문에 위에서 내려오려면 위 좌표의 위에서 쭉 내려오는 방법(dp[i-1][j][0])밖에 없기 때문에 dp[i][j][0]은 그대로 dp[i-1][j][0]와 같다.
- .마찬가지로 왼쪽에서 오는 방법(dp[i][j][1])을 보면 왼쪽의 좌표(cityMap[i][j-1])가 0이라면 왼쪽 좌표의 왼쪽에서 온 방법 (dp[i][j-1][1])과 왼쪽 좌표의 위에서 온 방법(dp[i][j-1][0])에서 오른쪽으로 오면 되는 것이기 때문에 두 방법을 더하고(dp[i][j-1][0] + dp[i][j-1][1]) 수가 커질 수 있기 때문에 20170805로 나눈 나머지를 저장한다.
- 또한 왼쪽 좌표(cityMap[i][j-1])가 2라면 왼쪽 좌표에서 좌회전과 우회전이 되지 않기 때문에 왼쪽 좌표에서 해당 오른쪽 좌표로 오는 방법은 왼쪽 좌표의 왼쪽에서 쭉 직선으로 오는 방법(dp[i][j-1][1])밖에 없기 때문에 dp[i][j][1]는 그대로 dp[i][j-1][1]와 같다.
- 이렇게 도착점까지 dp를 모두 업데이트한 후에 도착점의 왼쪽에서 오는 방법과 위쪽에서 오는 방법을 더한(dp[m-1][n-1][0] + dp[m-1][n-1][1]) 후에 20170805로 다시 한 번 나눈 나머지를 answer에 저장하고 반환하면 된다.
'Programmers' 카테고리의 다른 글
| [프로그래머스 Level.3] 광고 삽입 (2021 KAKAO BLIND RECRUITMENT) (Java) (0) | 2023.03.24 |
|---|---|
| [프로그래머스 Level.3] 자물쇠와 열쇠 (2020 KAKAO BLIND RECRUITMENT) (Java) (0) | 2023.03.22 |
| [프로그래머스 Level.2] 리코쳇 로봇 (연습문제) (Java) (0) | 2023.03.20 |
| [프로그래머스 Level.3] 부대복귀 (연습문제) (Java) (0) | 2023.03.19 |
| [프로그래머스 Level.3] [1차] 셔틀버스 (2018 KAKAO BLIND RECRUITMENT) (Java) (0) | 2023.03.17 |
![[프로그래머스 Level.3] 보행자 천국 (2017 카카오코드 예선) (Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fb15uw1%2Fbtr49TV9jI5%2FEATpCzqA7UhVFrhxSN7M7K%2Fimg.png)